A Brief Introduction to Lawson Numbers
As recently announced, Alexander (Sandy) Lawson is the winner of the 2011 Herman Skolnik Award. According to the announcement, among Lawson's recognized achievements is the development of Lawson Numbers as part of the Beilstein System:
As early aids to searching in Beilstein, he developed the Lawson Number and the SANDRA program. He was instrumental in the creation and development of the electronic Beilstein Database, including both the organization, data structure, and indexing, and also the development of the powerful CrossFire search engine and interface, capable of handling millions of molecules, reactions, and properties.
I have to admit to drawing a blank on reading the term "Lawson Number". I've heard the term before, but what are Lawson Numbers and why should anybody care? This article assembles a few of my notes in researching this intriguing molecular classification system. It is likely full of errors as there appears to be no authoritative, publicly-viewable documentation on Lawson Numbers. If you post a comment correcting me with a reference, I'll update this article accordingly.
The Problem
Lawson Numbers were developed to enable the Beilstein System to break up organic chemical space into a limited number of roughly equally-populated sections containing related structures. Why? Printed Beilstein developed a registry system that made it possible to find the volume and page a structure should appear in without the need for a computer. Lawson Numbers (originally implemented in the program SANDRA) enabled the automated placement of structures into the Beilstein Registry.
Lawson Numbers are structural hashcodes with a twist.
A Fuzzy Identifier
A Lawson Number is a non-unique structural identifier in that the same structure can be assigned multiple Lawson Numbers. Here's a breakdown in 1991, a time at which Beilstein contained 1.8 million structures:
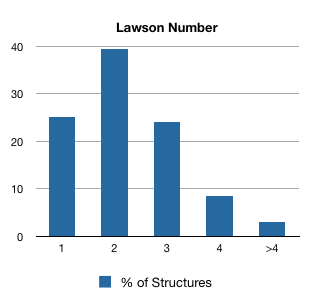
As you can see, most structure have two or more Lawson Numbers, although the number rarely exceeds four.
Range
A Lawson Number is an unsigned integer up to 32767. A planned extension to enable larger Lawson Numbers never materialized.
Use
The main use for Lawson Numbers appears to have been as a compliment to substructure searching. You might be looking for a synthesis of a particular pyridinecarboxylate ester and find none. As a fictitious example, using the Lawson Numbers for your specific structure might enable you to find preparations of related heteroaryl carboxylate esters.
In the Beilstein System, Lawson Numbers are searchable fields like molecular weight. So you might use Lawson Numbers in combination with molecular weight or name fragment filters to refine your search. You might then use some of the Lawson Numbers in that search to broaden your search a bit, and so on, until you finally find a synthesis that is close enough to the one you want to accomplish.
References
The documentation on Lawson Numbers is quite sparse, but there are some good resources. Some are:
- 2004 Slides by Gary Wiggins and Usha Coca
- The Beilstein Handbook of Organic Chemistry for the Occasional User
- Lawson Number (LN)
One potentially useful paper is unfortunately hidden behind a publisher paywall:
Conclusions
Fuzzy searches of chemical structure databases can be powerful compliments to old mainstay of substructure searching. Although the underlying technology behind Lawson Numbers appears to be a trade secret, the concept is simple: provide a way to assign multiple hashcodes to the same structure, and ensure that those hashcodes represent well-defined structural boundaries. Like other technologies developed during the golden age of cheminformatics which have subsequently fallen out of favor, Lawson Numbers may be worth taking a second look at.
Lawson Numbers were developed when information capacity was measured in inches and pounds, publication resulted in trees dying, and interactivity meant talking to a librarian. What would be the tradeoffs of a Lawson-like system supporting millions or billions of hashcodes and dozens or hundreds of hashcodes for each structure? What if you could choose hashcode properties on the fly? What if you could graphically 'surf' these hashcodes from island to island of organic structural similarity?
Food for thought.